lunes, 9 de julio de 2012
4.7 Calcuo de Integrales Expresadas como Serie de Taylor
Cálculo de integrales expresadas como serie de Taylor
Si esta serie converge
para todo x perteneciente al intervalo
(a-r, a+r) y la suma es igual a f(x),
entonces la función f(x) se llama analítica. Para comprobar
si la serie converge a f(x), se suele utilizar una estimación del
resto del teorema de Taylor. Una
función es analítica si y solo si se puede representar con una serie de
potencias; los coeficientes de esa serie son necesariamente los determinados en
la fórmula de la serie de Taylor.
Si a = 0, a la
serie se le llama serie de Maclaurin.
Esta representación
tiene tres ventajas importantes:
- La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.
- Se puede utilizar para calcular valores aproximados de la función.
- Es posible demostrar que, si es viable la transformación de una función a una serie de Taylor, es la óptima aproximación posible.
Suscribirse a:
Enviar comentarios (Atom)


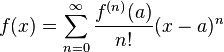
0 comentarios:
Publicar un comentario