lunes, 9 de julio de 2012
4.7 Calcuo de Integrales Expresadas como Serie de Taylor
Cálculo de integrales expresadas como serie de Taylor
Si esta serie converge
para todo x perteneciente al intervalo
(a-r, a+r) y la suma es igual a f(x),
entonces la función f(x) se llama analítica. Para comprobar
si la serie converge a f(x), se suele utilizar una estimación del
resto del teorema de Taylor. Una
función es analítica si y solo si se puede representar con una serie de
potencias; los coeficientes de esa serie son necesariamente los determinados en
la fórmula de la serie de Taylor.
Si a = 0, a la
serie se le llama serie de Maclaurin.
Esta representación
tiene tres ventajas importantes:
- La derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales.
- Se puede utilizar para calcular valores aproximados de la función.
- Es posible demostrar que, si es viable la transformación de una función a una serie de Taylor, es la óptima aproximación posible.
4.6 Representaciòn de funciones mediante las serie de taylor
Sea f(x) una función definida en un intervalo que
contiene al punto a, con derivada de todos los órdenes.
El polinomio de primer grado p1(x) = f(a) +
f ' (a) (x-a) tiene el mismo valor que f(x) en el punto x=a y
también, como se comprueba fácilmente, la misma derivada que f(x) en este punto.
Su gráfica es una recta tangente a la gráfica de f(x) en el punto
a.
Es posible elegir un polinomio de segundo grado,
p2(x) = f(a) + f ' (a) (x-a) + ½ f ' ' (a) (x-a)2,
tal que en el punto x=a tenga el mismo valor que f(x) y valores también iguales
para su primera y segunda derivadas. Su gráfica en el punto a se acercará a la
de f(x) más que la anterior. Es natural esperar que si construimos un polinomio
que en x=a tenga las mismas n primeras derivadas que f(x) en el mismo punto,
este polinomio se aproximará más a f(x) en los puntos x próximos a a. Así
obtenemos la siguiente igualdad aproximada, que es la fórmula de
Taylor:
f(x) ≈ f(a) + f '(a) (x-a) + (1/2!) f ' '(a)
(x-a)2 + ...... + (1/n!) f (n)(a)
(x-a) n
El segundo miembro de esta fórmula es un polinomio de
grado n en (x-a). Para cada valor de x puede calcularse el valor de este
polinomio si se conocen los valores de f(a) y de sus n primeras
derivadas.
Para funciones que tienen derivada (n+1)-ésima, el
segundo miembro de esta fórmula, como se demuestra fácilmente, difiere del
primero en una pequeña cantidad que tiende a cero más rápidamente que
(x-a)n. Además, es el único polinomio de grado n que difiere de f(x),
para x próximo a a, en un valor que tiende a cero (cuando x tiende a a) más
rápidamente que (x-a)n.
Si f(x) es un polinomio algebraico de grado n, entonces la igualdad aproximada anterior es una verdadera igualdad.
Si f(x) es un polinomio algebraico de grado n, entonces la igualdad aproximada anterior es una verdadera igualdad.
Para que sea exacta la igualdad aproximada anterior,
debemos añadir al segundo miembro un término más, llamado resto:
f(x) = f(a)+f '(a)(x-a)+(1/2!) f ' '(a)(x-a)2+
...... +(1/n!) f (n)(a)(x-a)n+(1/(n+1)!)
f (n+1)(c)(x-a)n+1
El resto tiene la peculiaridad de que la derivada que en
él aparece debe calcularse en cada caso, no en el punto a, sino en un punto c
convenientemente elegido, desconocido, pero interior al intervalo de extremos a
y x.
La demostración de la igualdad anterior es bastante
engorrosa, aunque sencilla en esencia.
Las leyes naturales pueden expresarse, por regla general,
con buena aproximación por funciones derivables un número arbitrario de veces, y
por ello pueden ser aproximadas por polinomios cuyo grado viene determinado por
la precisión deseada.
La fórmula de Taylor, que abre el camino para la mayoría
de los cálculos en el análisis aplicado, es muy importante desde el punto de
vista práctico.
La idea de aproximar una función mediante polinomios o de
representarla como suma de un número finito de funciones más sencillas alcanzó
un gran desarrollo en el análisis, donde constituye ahora una rama
independiente: la teoría de la aproximación de funciones.
En el enlace siguiente de Fuente se encuentran ejemplos
realizados para comprender mejor la aproximacion en Series de
Taylor.
4.5 Serie de Taylor
Calculo de Integrales de funciones expresadas como Serie de Taylor
La
función p(x)=a0+a1x+a2x2+..........+anxn,
en la que los coeficientes ak son constantes, se llama polinomio de
grado n. En particular y=ax+b es un polinomio de primer grado e
y=ax2+bx+c es un polinomio de segundo grado. Los polinomios
pueden considerarse las funciones más sencillas de todas. Para calcular su valor
para una x dada, necesitamos emplear únicamente las operaciones de adición,
sustracción y multiplicación; ni siquiera la división es necesaria. Los
polinomios son funciones continuas para todo x y tienen derivadas de cualquier
orden. Además la derivada de un polinomio es también un polinomio de grado
inferior en una unidad, y las derivadas de orden n+1 y superiores de un
polinomio de grado n son nulas.
Si a los polinomios añadimos las funciones de la forma
y=p(x)/q(x) (cociente de polinomios, para cuyo cálculo necesitamos
también de la división), las funciones raíz cuadrada de x y raíz cúbica de x, y
finalmente, las combinaciones aritméticas de los tipos anteriores, obtenemos
esencialmente las funciones cuyos valores pueden calcularse por métodos
aprendidos en el bachillerato.
A este nivel se tienen nociones de algunas otras
funciones tales como log(x), sen(x), ex, ..., pero, aunque se
estudian sus propiedades más importantes, no se da una respuesta a las
preguntas: ¿Cómo calcularlas? ¿Qué clase de operaciones, por ejemplo, es
necesario realizar sobre la x para obtener log(x) o sen(x)?. La respuesta a
estas preguntas la proporcionan los métodos desarrollados por el análisis
matemático.
4.4 RADIO DE CONVERGENCIA
En matemáticas según el
teorema de Cauchy-Hadamard el radio de convergencia de una serie de la forma  ,
con
,
con  ,
viene dado por la expresión:
,
viene dado por la expresión:
 ,
con
,
con  ,
viene dado por la expresión:
,
viene dado por la expresión:
DEFINICION
Si nos
limitamos al conjunto de los números reales una serie de la forma  ,
con
,
con  ,
recibe el nombre de serie de potencias centrada en x0. La serie converge
absolutamente para un conjunto de valores de x que verifica que |
x − x0 | <
r, donde r es un número real llamado radio de
convergencia de la serie. Esta converge, pues, al menos, para los valores de
x pertenecientes al intervalo (x0 −
r, x0 + r), ya que la
convergencia para los extremos de este ha de estudiarse aparte, por lo que el
intervalo real de convergencia puede ser también semiabierto o cerrado. Si la
serie converge solo para x0, r = 0. Si lo hace para cualquier valor de
x, r
=
,
recibe el nombre de serie de potencias centrada en x0. La serie converge
absolutamente para un conjunto de valores de x que verifica que |
x − x0 | <
r, donde r es un número real llamado radio de
convergencia de la serie. Esta converge, pues, al menos, para los valores de
x pertenecientes al intervalo (x0 −
r, x0 + r), ya que la
convergencia para los extremos de este ha de estudiarse aparte, por lo que el
intervalo real de convergencia puede ser también semiabierto o cerrado. Si la
serie converge solo para x0, r = 0. Si lo hace para cualquier valor de
x, r
= 
 ,
con
,
con  ,
recibe el nombre de serie de potencias centrada en x0. La serie converge
absolutamente para un conjunto de valores de x que verifica que |
x − x0 | <
r, donde r es un número real llamado radio de
convergencia de la serie. Esta converge, pues, al menos, para los valores de
x pertenecientes al intervalo (x0 −
r, x0 + r), ya que la
convergencia para los extremos de este ha de estudiarse aparte, por lo que el
intervalo real de convergencia puede ser también semiabierto o cerrado. Si la
serie converge solo para x0, r = 0. Si lo hace para cualquier valor de
x, r
=
,
recibe el nombre de serie de potencias centrada en x0. La serie converge
absolutamente para un conjunto de valores de x que verifica que |
x − x0 | <
r, donde r es un número real llamado radio de
convergencia de la serie. Esta converge, pues, al menos, para los valores de
x pertenecientes al intervalo (x0 −
r, x0 + r), ya que la
convergencia para los extremos de este ha de estudiarse aparte, por lo que el
intervalo real de convergencia puede ser también semiabierto o cerrado. Si la
serie converge solo para x0, r = 0. Si lo hace para cualquier valor de
x, r
= 
Ejemplos
Mostraremos
el radio de convergencia de algunos desarrollos en series de potencias con sus
respectivos radios de convergencia sin justificar porqué el radio de
convergencia es el dado.
RADIO DE CONVERGENCIA FINITO
La función
1 / (1 − x) en su desarrollo con centro 0, o
sea, en series de potencia x − x0 = x − 0 = x,
tiene el siguiente aspecto:
 .
.
(para el
cálculo de la serie vea serie de Taylor). Su
radio de convergencia es r = 1. Eso
significa que para calcular si tomo cualquier valor cuya distancia al x0 =
0 es menor que r = 1, por ejemplo el
x = 0.25, entonces al remplazarlo en la serie
el resultado de calcular la serie será el mismo que remplazarlo en la función,
de hecho
 .
.
(la cuenta
se puede hacer por serie de potencia). Y por otro lado
 .
.
Pero si
tomamos un elemento fuera del radio de convergencia, por ejemplo el x = 2, los más probable es que al remplazarlo en la
serie, ésta diverja (por eso el nombre de radio de convergencia).
Efectivamente:
 .
.DISTGANCIA DE SEGURIDAD
El cálculo
del radio de convergencia no es simple. Veamos una función con dos desarrollos
en serie con distintos centros y analicemos sus radios de convergencia. La misma
función 1 / (1 − x) en su desarrollo con
centro x0 = 3 tiene la
forma:
 .
.
Pero en este
caso su radio de convergencia es r = 2.
Notemos que la función 1 / (1 − x) tiene una
singularidad en el 1; y que en los dos caso anteriores el radio de convergencia
coincide con la distancia del centro a la singularidad: | 0
− 1 | = 1 y | 3 − 1 | = 2. Esto será siempre
verdadero para ésta función, pero, no puede generalizarse, como veremos en el
siguiente ejemplo:
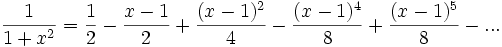
Como no hay
singularidades reales podría suponerse que el radio es infinito, sin embargo su
radio de convergencia es  .
Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la
función a dominio complejo, existe una singularidad en el denominador.La
serie
.
Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la
función a dominio complejo, existe una singularidad en el denominador.La
serie
 .
Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la
función a dominio complejo, existe una singularidad en el denominador.La
serie
.
Este radio parece caprichoso pero tiene que ver con el hecho de que pasando la
función a dominio complejo, existe una singularidad en el denominador.La
serieRADIO DE CONVERGENCIA INFINITO
Por ejempo,
la función ex puede desarrollarse en
series de potencia de x − 0 = x, de
hecho  .
.
 .
.
y esto vale
para todo real x por eso el radio de
convergencia será infinito
4.2.1 Series de Potencia
Serie de potencias
Definición
Una serie de potencias alrededor de x=0 es una serie de la forma:Una serie de potencias alrededor de x=c es una serie de la forma:
En el cual el centro es c, y los coeficientes
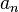 son los términos de una sucesion.
son los términos de una sucesion.Ejemplos
- La serie geométrica
 es una serie de potencias absolutamente convergente si
es una serie de potencias absolutamente convergente si  y divergente si
y divergente si  ó
ó 
- La serie de potencias
 es absolutamente convergente para todo
es absolutamente convergente para todo 
- La serie de potencias
 solamente converge para
solamente converge para 
4.2 Serie Numerica y convergencia
4.1.2 Series Infinitas (Criterio de D' Lembert)(Criterio de Cauchy)
Criterio D' Lembert
Definiendo
con n a la variable independiente de la sucesión, dicho criterio establece que
si llamamos L al límite para n tendiendo a infinito de se obtiene un número L,
con los siguientes
Si
L = 1, el criterio no decide y es necesario calcular el límite de otro
modo.
El criterio de D'Alembert se utiliza para clasificar las series numéricas. Podemos enunciarlo de la siguiente manera:
Tal
que:
f(n)
> 0 (o sea una sucesión de terminos positivos) y
f(n) tienda a cero cuando n tiende a infinito (condición necesaria de convergencia)
Se procede de la siguiente manera:
f(n) tienda a cero cuando n tiende a infinito (condición necesaria de convergencia)
Se procede de la siguiente manera:
con
n tendiendo a infinito.
Así
obtenemos L y se clasifica de la siguiente manera:
L
< 1 la serie converge
L > 1 la serie diverge
L = 1 el criterio no sirve hay que aplicar otro criterio.
L > 1 la serie diverge
L = 1 el criterio no sirve hay que aplicar otro criterio.
Acontinuacion
se muestra un breve Ejemplo:
Criterio de Cauchy
Entonces, si:
L
< 1, la serie es convergente.
L > 1 entonces la serie es divergente.
L=1, no podemos concluir nada a priori y tenemos que recurrir al criterio de Raabe,
o de comparación, para ver si podemos llegar
L > 1 entonces la serie es divergente.
L=1, no podemos concluir nada a priori y tenemos que recurrir al criterio de Raabe,
o de comparación, para ver si podemos llegar
4.1.1 Series Finitas
Donde D denota
el operador derivada, que hace corresponder  con
su derivada
con
su derivada  ,
es decir,
,
es decir, 
 con
su derivada
con
su derivada  ,
es decir,
,
es decir, 
Formalmente,
invirtiendo la exponencial,
Esta
fórmula sigue siendo válida en el sentido de que ambos operadores dan el mismo
resultado cuando se aplican a un polinomio.
Incluso para funciones analíticas, las series de la derecha no convergen con
seguridad, sino que puede tratarse de una serie asintótica.
Sin embargo, pueden emplearse para obtener aproximaciones más precisas de la
derivada. Por ejemplo, Los dos primeros términos de la serie llevan a:
El
error de la aproximación es del orden de h2.
Las
fórmulas análogas para los operadores posterior y central son
UNIDAD IV
Definición de serie
Las series son una parte esencial en el campo de las Matemáticas.
Aunque se define simplemente como la suma de términos finitos o infinitos, tiene una gran importancia.
Una serie finita termina finitamente, esto es, tiene definido tanto el primer como elúltimotérmino.
Por otro lado, una serie infinita continúa sin interrupción.
Por ejemplo: {1, 3, 6, 8} se puede considerar como una serie finita, mientras que una serie de la forma {2, 4, 6 8…} es un ejemplo de serie infinita.
En algunos casos, es beneficioso convertir un número o una función en forma de series infinitas lo cual a su vez puede ayudar en su cálculo.
Incluso puede lograr que el cálculo complejo sea más fácil.
Por ejemplo, para el cálculo exponencial, este puede ser convertido en la forma:

Esta técnica de expansión puede ser utilizada eficazmente con el fin de obtener los valores estimados de la función, de las integrales o para resolver ecuaciones diferenciales, algebraicas o integrales.
Cuando la serie infinita es reemplazada por la suma de los términos inicialesde la serie, un valor de error aproximado puede ser estimado, lo que a su vez, ayuda en la determinación de la razón de convergencia efectiva para la serie correspondiente.
Las series pueden ser convergentes o divergentes. Una serie convergente tiene las siguientes propiedades:
1) Si el término parcial de la sucesión de la serie converge, entonces se dice que toda la serie es convergente. Por otro lado, si el término parcial de lasucesión diverge, la serie también diverge.
2) En caso que el resto de alguna parte de la serie converja, entonces toda la serie converge y viceversa.
3) Si una serie de la forma  converge, entonces la serie de la forma
converge, entonces la serie de la forma  converge también.
converge también.
 converge, entonces la serie de la forma
converge, entonces la serie de la forma  converge también.
converge también.
4) Si la serie de la forma  converge, entonces la serie de la forma
converge, entonces la serie de la forma  converge.
converge.
 converge, entonces la serie de la forma
converge, entonces la serie de la forma  converge.
converge.
5) La serie  converge, sólo con la condición de que
converge, sólo con la condición de que  también converja.
también converja.
 converge, sólo con la condición de que
converge, sólo con la condición de que  también converja.
también converja.
6) Se dice que una serie de la forma  es convergente si α> 1 y diverge en el caso inverso, es decir, cuando α<1.
es convergente si α> 1 y diverge en el caso inverso, es decir, cuando α<1.
 es convergente si α> 1 y diverge en el caso inverso, es decir, cuando α<1.
es convergente si α> 1 y diverge en el caso inverso, es decir, cuando α<1.
Puede suceder el caso que la suma de las series sea desconocida.
En ese caso, la condición de Cauchy puede ser utilizada con el fin de encontrar la convergencia de la serie.
De acuerdo con la condición de Cauchy, existe un número n∊para cada ∊> 0, el cual satisface la condición  , n>nε. Aquí p es un entero positivo.
, n>nε. Aquí p es un entero positivo.
 , n>nε. Aquí p es un entero positivo.
, n>nε. Aquí p es un entero positivo.
Una serie que contiene los términos positivos tiene su importancia en la teoría de las series.
Una condición necesaria e importante para que estos tipos de seriessean convergentes es que la sucesión de la suma parcial debe ser limitada.
Por otro lado, si se cumple la condición  , entonces la serie diverge.
, entonces la serie diverge.
 , entonces la serie diverge.
, entonces la serie diverge.
Veamos un ejemplo del concepto de series convergentes y divergentes. Suponga que la forma de la seriees .
Con el fin de determinar si la serie dada converge o diverge, lo primero y más importante a determinar es si la suma parcial de la sucesión diverge o converge. La suma parcial de la sucesión parala serie correspondiente puede ser dada como  . Se puede observar que el límite de los términos de la suma parcial es divergente al infinito
. Se puede observar que el límite de los términos de la suma parcial es divergente al infinito  .
.
 . Se puede observar que el límite de los términos de la suma parcial es divergente al infinito
. Se puede observar que el límite de los términos de la suma parcial es divergente al infinito  .
.
Por lo tanto, se dice que toda la serie es divergente
Suscribirse a:
Entradas (Atom)


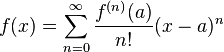

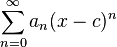












 - \frac12 \Delta^2[f](x)}{h} = - \frac{f(x+2h)-4f(x+h)+3f(x)}{2h}.](http://upload.wikimedia.org/math/2/7/b/27b822c687681955e82cb52e60f2d5cb.png)
